Graph algorithms
Most of my research fits into the broad spectrum of graph-based algorithms. Below are a number of specific fields of research where I both develop and use graph-based algorithms.
Stable Matching Problems
A matching to a stable matching problem is stable if, given some agents with preferences, no pair of agents will both prefer to break with the given matching. These types of matchings are applicable to the allocation of people and/or resources, including assigning junior doctors to training positions at hospitals or teachers to schools. These preferences can come with some of the following properties:
- ties — these happen if an agent cannot sufficiently differentiate between two or more options, and
- incompleteness — some options may be unsuitable or unacceptable, or a person may not wish to offer preferences over all options, so they present an incomplete list of preferences over only some options.
If both ties and incompleteness are present, then finding a stable matching of largest size is NP-Hard. I have worked on preprocessing techniques and models for solving such problems, and am very interested in the specific parameters or structures of when such problems become hard, in both theoretic and practical senses.
Graph Decompositions
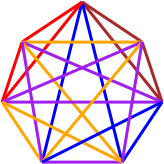
A graph decomposition is (often) a partitioning of the edge set of the graph into some distinct sets, often represented by colours. A graph factorisation is a specific type of decomposition, wherein each set must be incident to every vertex. I study the existence of these decompositions and factorisations of
- complete graphs
- bi-partite graphs
- circulant graphs and
- multigraphs.
Multi-objective optimisation
In multi-objective optimisation, we are searching for a "good" solution to a given problem given a number of distinct criteria that are often in competition with each other. I have designed and implemented many multi-objective integer optimisation algorithms to solve such problems far faster. This is achieved through the use of parallel techniques and online communication between workers.
Combinatorial and computational topology

Topology is the study of shapes without distances. We allow these shapes to be squished and stretched, as long as we don't poke holes in the shapes. Topologists are often said to be unable to differentiate between a cup and a donut.
I am part of the development team for Regina, a mathematical software suite for 3-manifold topologists. As part of this, I have worked on:
- Census enumeration algorithms, and their complexity
- Calculations of quantum invariants
- Algorithms on triangulations
- Spine codes of 3-manifolds
- Properties of Pachner graphs